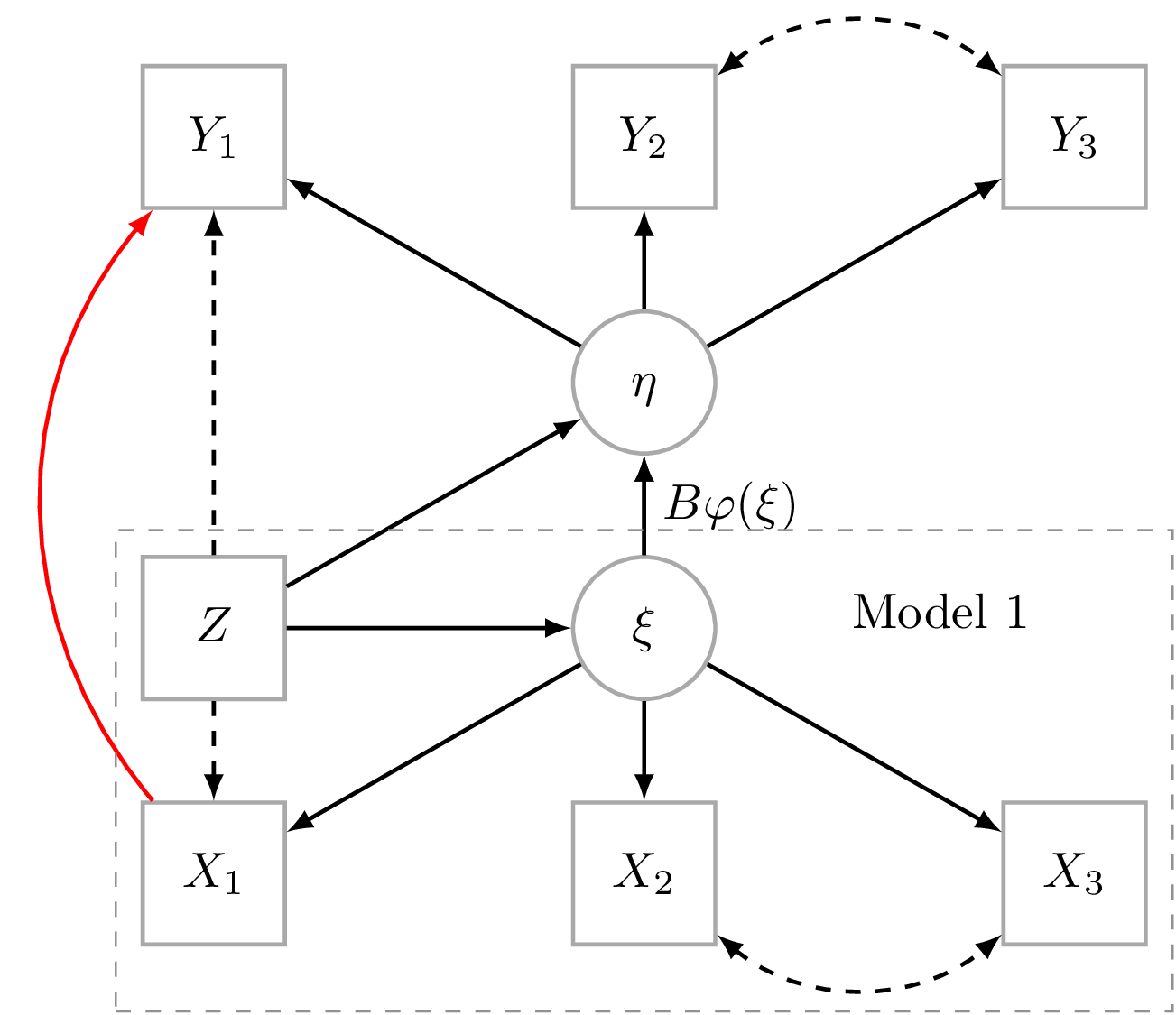
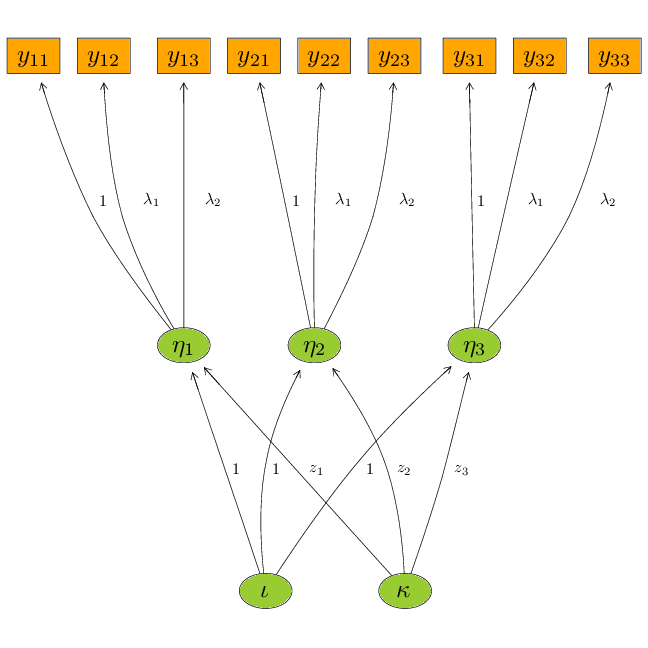
Latent Variable Model

ML-inference in non-linear SEMs is complex. Computational intensive methods based on numerical integration are needed and results are sensitive to distributional assumptions. In a recent paper: A two-stage estimation procedure for non-linear structural equation models by Klaus Kähler Holst & Esben Budtz-Jørgensen (https://doi.org/10.1093/biostatistics/kxy082), we consider two-stage estimators as a computationally simple alternative to MLE. Here both steps are based on linear models: first we predict the non-linear terms and then these are related to latent outcomes in the second step. ...

Applications of structural equation models (SEMs) are often restricted to linear associations between variables. Maximum likelihood (ML) estimation in non-linear models may be complex and require numerical integration. Furthermore, ML inference is sensitive to distributional assumptions. In this paper, we introduce a simple two-stage estimation technique for estimation of non-linear associations between latent variables. Here both steps are based on fitting linear SEMs: first a linear model is fitted to data on the latent predictor and terms describing the non-linear effect are predicted by their conditional means. In the second step, the predictions are included in a linear model for the latent outcome variable. We show that this procedure is consistent and identifies its asymptotic distribution. We also illustrate how this framework easily allows the association between latent variables to be modelled using restricted cubic splines and we develop a modified estimator which is robust to non-normality of the latent predictor. In a simulation study, we compare the proposed method to MLE and alternative two-stage estimation techniques.

An R package for specifying and estimating linear latent variable models is presented. The philosophy of the implementation is to separate the model specification from the actual data, which leads to a dynamic and easy way of modeling complex hierarchical structures. Several advanced features are implemented including robust standard errors for clustered correlated data, multigroup analyses, non-linear parameter constraints, inference with incomplete data, maximum likelihood estimation with censored and binary observations, and instrumental variable estimators. In addition an extensive simulation interface covering a broad range of non-linear generalized structural equation models is described. The model and software are demonstrated in data of measurements of the serotonin transporter in the human brain.